阿力的迷宫 1076
Time Limit: 1 Sec
Memory Limit: 256 MB
Submission：0
AC：0
Score：100
Description
阿力打算修建一座这样的迷宫：
迷宫可以看成n个点，nm条边的有向图。1号点是唯一的入口与出口。
每一个点恰好有 m条出边，且这些出边被依次标号为[0,m)的正整数。
迷宫允许自环和重边。
同时，一座优秀的迷宫应该有一定的解谜因素。因此阿力希望每一条从1号点出发并回到1号点的回路都有着一定的规律。
阿力发现，如果把一条从1出发的路径经过的所有边的编号都记录下来，那么能得到一个（可能有前导0）的m进制数；同时对于每一个（可能有前导0）的m进制数，都能对应回一条从1出发的路径。
于是阿力选定了一个整数k，他希望这个迷宫满足一条从1出发的路径能回到1当且仅当这条路径对应的数是k的倍数。
现在阿力已经选定了m和k，但是他发现并不是对所有的n，都存在满足上述所有条件的迷宫设计方案。建造迷宫是一件费时费力的事情，于是阿力想要找到一个最小的满足条件的n。
迷宫可以看成n个点，nm条边的有向图。1号点是唯一的入口与出口。
每一个点恰好有 m条出边，且这些出边被依次标号为[0,m)的正整数。
迷宫允许自环和重边。
同时，一座优秀的迷宫应该有一定的解谜因素。因此阿力希望每一条从1号点出发并回到1号点的回路都有着一定的规律。
阿力发现，如果把一条从1出发的路径经过的所有边的编号都记录下来，那么能得到一个（可能有前导0）的m进制数；同时对于每一个（可能有前导0）的m进制数，都能对应回一条从1出发的路径。
于是阿力选定了一个整数k，他希望这个迷宫满足一条从1出发的路径能回到1当且仅当这条路径对应的数是k的倍数。
现在阿力已经选定了m和k，但是他发现并不是对所有的n，都存在满足上述所有条件的迷宫设计方案。建造迷宫是一件费时费力的事情，于是阿力想要找到一个最小的满足条件的n。
Input
第一行输入一个整数 t表示数据组数。
接下来t行每行两个十进制正整数m,k表示阿力选定的整数。
接下来t行每行两个十进制正整数m,k表示阿力选定的整数。
Output
对于每组数据，输出一行一个整数表示能够满足所有条件的最小的n 。如果不存在这样的n ，输出 -1。
Samples
input:
3
2 3
2 4
6 8
output:
3
3
5
Hint
第一组数据图
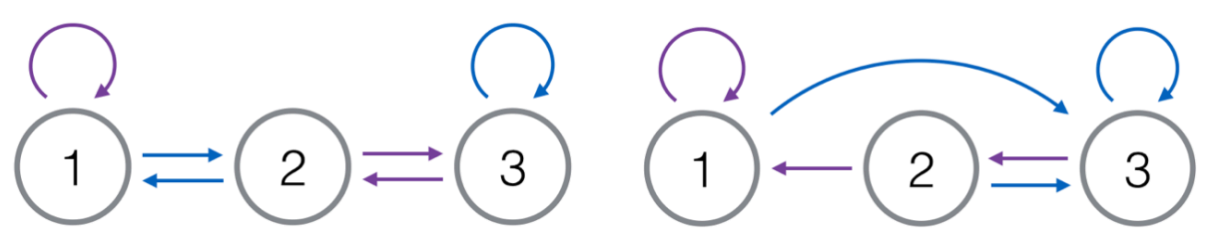第二组数据图